Matematicas

 DEFINICION DE SUCESION NUMERICA REAL

 En análisis matemático y en álgebra, una sucesión es una aplicación cuyo dominio es el conjunto de los números naturales y su dominio es cualquier otro conjunto, generalmente de números de diferente naturaleza, también pueden ser figuras geométricas o funciones. Cada uno de ellos es denominado término (también elemento o miembro) de la sucesión y al número de elementos ordenados (posiblemente infinitos) se le denomina la longitud de la sucesión. No debe confundirse con una serie matemática, que es la suma de los términos de una sucesión.

A diferencia de un conjunto, el orden en que aparecen los términos sí es relevante y un mismo término puede aparecer en más de una posición. De manera formal, una sucesión puede definirse como una función sobre el conjunto de los números naturales (o un subconjunto del mismo) y es por tanto una función discreta.

Video Explicativo

Ejemplos 

PROGRESIONES ARITMETICAS 

Una progresión aritmética es una sucesión de números tales que la diferencia de cualquier par de términos sucesivos de la secuencia es constante, dicha cantidad llamada «diferencia de la progresión», «diferencia» o incluso «distancia».

En una progresión aritmética, si se toman dos términos consecutivos de cualquiera de esta, la diferencia entre ambos es una constante, denominada diferencia. Esto se puede expresar como una relación de recurrencia de la siguiente manera:

${\displaystyle a_{n+1}-a_{n}=d}$.

Conociendo el primer término a₁ y la diferencia d, se puede calcular el enésimo término de la progresión mediante sustitución sucesiva en la relación de recurrencia

${\displaystyle a_{1},\,\underbrace {(a_{1}+d)} _{a_{2}},\,(\underbrace {\underbrace {a_{1}+d} _{a_{2}}+d} _{a_{3}}),\,\cdots \,,\,(\underbrace {\underbrace {a_{1}+(n-2)d} _{a_{n-1}}+d} _{a_{n}})}$

con lo que se obtiene una fórmula para el término general de una progresión aritmética, escrita de manera compacta como:

${\displaystyle a_{n}=a_{1}+{(n-1)}{d}\,}$

donde d es un número real cualquiera.

También se puede escribir el término general de otra forma. Para ello se consideran los términos a_m y a_n (m<n) de la progresión anterior y se ponen en función de a₁:

${\displaystyle {\begin{matrix}a_{m}=&a_{1}+(m-1)d\\a_{n}=&a_{1}+(n-1)d\end{matrix}}}$

Restando ambas igualdades, y trasponiendo, se obtiene:

${\displaystyle a_{n}=a_{m}+(n-m)d\,}$

expresión más general que (I), pues da los términos de la progresión conociendo uno cualquiera de ellos, y la diferencia.

Ejemplo

VARIABLES ALEATORIAS

Una variable aleatoria es una función que asigna un valor, usualmente numérico, al resultado de un experimento aleatorio. Por ejemplo, los posibles resultados de tirar un dado dos veces: (1, 1), (1, 2), etc. o un número real ( la temperatura máxima medida a lo largo del día en una ciudad concreta).

Los valores posibles de una variable aleatoria pueden representar los posibles resultados de un experimento aún no realizado, o los posibles valores de una cantidad cuyo valor actualmente existente es incierto ( como resultado de una medición incompleta o imprecisa). Intuitivamente, una variable aleatoria puede tomarse como una cantidad cuyo valor no es fijo pero puede tomar diferentes valores; una distribución de probabilidad se usa para describir la probabilidad de que se den los diferentes valores. En términos formales una variable aleatoria es una función definida sobre un espacio de probabilidad.

Las variables aleatorias suelen tomar valores reales, pero se pueden considerar valores aleatorios como valores lógicos, funciones o cualquier tipo de elementos (de un espacio medible). El término elemento aleatorio se utiliza para englobar todo ese tipo de conceptos relacionados. Un concepto relacionado es el de proceso estocástico, un conjunto de variables aleatorias ordenadas (habitualmente por orden o tiempo).

                                          VIDEO

EJEMPLOS

TIPOS DE FUNCIONES: INYECTIVAS,SOBREYECTIVAS Y BIYECTIVAS

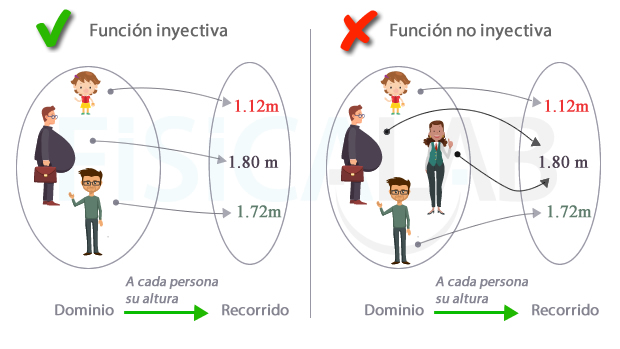
Funciones inyectivas

Una función es inyectiva cuando no hay dos elementos del dominio que tengan la misma imagen. Formalmente:

a,b∈Domf , si f(a)= f(b)⇒a=b

Es decir, para cualesquiera dos elementos a y b, pertenecientes al dominio de la función Domf, si sus imágenes f(a) y f(b) son iguales, los elementos son necesariamente iguales.

Funciones sobreyectivas

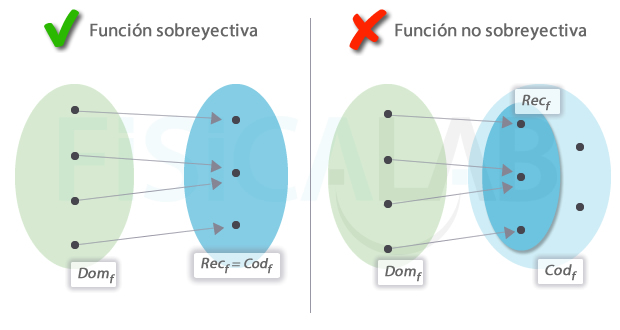
Una función es sobreyectiva, también llamada suprayectiva o exhaustiva, cuando el dominio y el recorrido coinciden. Formalmente:

∀y∈Codf ∃x∈Domf / f(x)=y

Es decir, para cualquier elemento y del codominio existe otro elemento x del dominio tal que y es la imagen de x por f.

Las funciones reales son sobreyectivas cuando Recf=ℝ, ya que, por definición, en ellas Codf=ℝ.

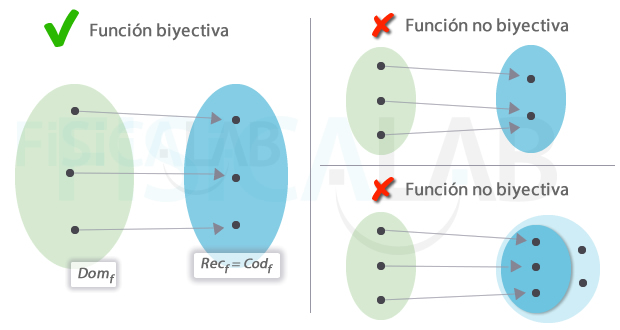
Funciones biyectivas

Una función es biyectiva, cuando es inyectiva y sobreyectiva al mismo tiempo. Formalmente:

y∈Codf ∃!x∈Domf / f(x)=y

Es decir, para cualquier elemento y del dominio existe un único elemento x del dominio tal que y es la imagen de x por f.

VIDEO

Ejemplos

f(x)=x+2−−−−−√3

f(x)=x+2−−−−−√

f(x)=2x3x2+1

f(x)=2x2x2+1

f(x)=ln(x)

f(x)=ex